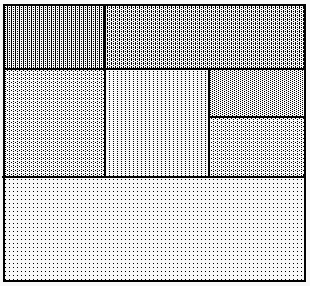
Figure 1: General Partition
[This article was originally published in PC AI magazine, Volume 13, Number 1 Jan/Feb 99. The magazine can be reached at PC AI, 3310 West Bell Rd., Suite 119, Phoenix AZ, USA 85023 Tel: (602) 971-1869, FAX: (602) 971-2321, E-Mail: [email protected], Web: http://www.pcai.com]

Figure 1: General Partition
If the surface is a sheet (of material) and the pieces are to be
cut from it, then the problem becomes the guillotine problem. The problem
takes its name from the necessity of cutting the sheet completely across
(like a guillotine) every time it is cut. Even if we only consider rectangular
pieces, as required in our domain, the problem has an exponential search
space. Each rectangle can be placed into any space large enough to hold
it, and, as can be seen in Figure 2, each rectangle not only has a size
but also an orientation.

Figure 2: Partition with one size Piece
The necessity of cutting the sheet all the way across limits the
number of combinations that have to be considered. That is, any configuration
with pieces bisected by the cut are illegal. Figure 1 would be a legal
configuration while Figure 2 would be illegal. This limiting of patterns
in conjunction with a small sheet size and a small number of pieces makes
the guillotine problem solvable for our domain.

Figure 3: Piece Input
The output of the system is a graphical display of the layout (Figure 4). The user then has the choice of letting the system run again to find a better answer or to use the current answer. After an answer is selected it can be printed to the default printer. We used line patterns for the pieces to differentiate them when printed on a black and white printer.
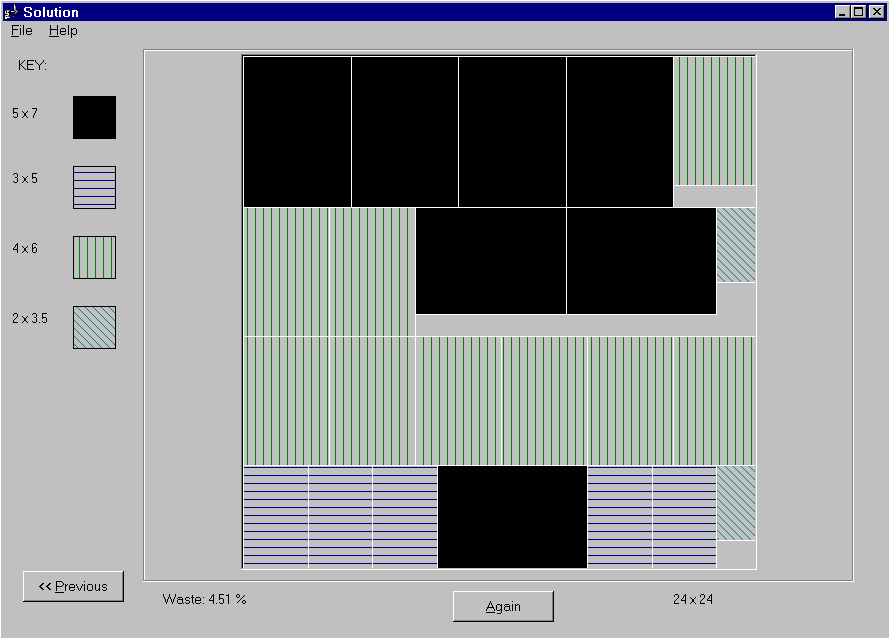
Figure 4: Graphical Display of Layout
The next section contains a more in- depth discussion of our use of generate and test.
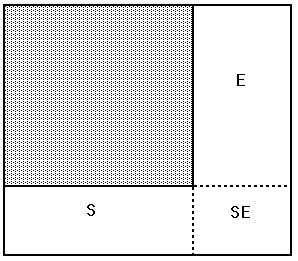
Figure 5: Placement of a Piece
is divided into smaller spaces whenever a piece is placed within
it: the part containing the piece, the part to the right (E) of the sheet,
the part below the piece (S), and the remainder of the space (SE). See
Figure 5. The program then adds the piece to the piece list and adds E
and the concatenation of S and SE to the spaces list (the concatenation
is allowed virtue of the guillotine).
This process continues until either all the pieces have been placed or none of the spaces in the space list are large enough to contain a piece. In the latter case, the procedure backtracks and tries a different configuration for the trial list. If none of the possible configurations are successful then it fails which causes a new trial list to be generated and the procedure restarts.
The logic engine returns a list of four-tuples representing the placement of the pieces (piece, orientation, upper left corner, lower right corner). While this is a correct answer to the problem it is not very useful. Were this (the logic engine) a stand alone program we would want to make two further improvements: to represent the answer in a useful manner (i.e., graphically) and to get user acceptance of the program without questioning our choice of language.
We could have done the graphics directly in Prolog though the best graphics package in Prolog lags somewhat behind other windows based languages such as Visual Basic, Visual C++ or Delphi. Visual Basic, for instance, allows a number of different scales (inches, centimeters, twips, ...), scaling of windows, the ability to reset coordinate systems and other useful graphics functions. Using Visual Basic also furthers our other goal of having the user accept the program because Visual Basic is a standard development system for Windows and therefore provides a comfortable, familiar environment for users. Adapting Visual Basic for the interface was rather straightforward as Amzi! Prolog has the "hooks" to allow it to be used as the inference engine for a Visual Basic front-end. In fact, Amzi! advertises what it calls a "Prolog sandwich"; a Prolog program embedded between C and Visual Basic. We believe that they are on the right track but just have not carried the idea through to completion.
The first question we usually encounter when explaining this approach is "why bother"? Obviously we could have written the whole guillotine program in Prolog. Why should we bother with Visual Basic or any other language? If there is only one programmer writing programs for their own use then there is no need to bother. However, if there is a team of programmers writing commercial programs then there are a number of reasons: the freedom for programmers to specialize in a language, the ability to easily create familiar looking applications, and a great speed-up in programming. The last point may need some defending, but picking the right tool for the job speeds up any job. Contrary to what their respective aficionados say, there is no perfect language. The reason people are using C (and C++) more and more is that it is capable of handling anything that needs to be done in a program. But there is a trade off in doing that. How many more hours would it take to produce a medium sized context free grammar in C then it would in Prolog? It could be written in C but why use C if Prolog were available? Likewise, if a program requires matrix manipulation why would Prolog be chosen? Each language has its strengths and weaknesses, by using the multi-paradigmatic approach the strengths are exploited while the weaknesses are avoided.
There is some overhead with the approach as each language has to have the capability and support for OLE, DDE and DLL. However more and more languages are being developed that do have that support. We have Prolog, Visual Basic, Lisp, Visual C++, Delphi and Smalltalk. Others, like APL and Scheme, are being developed. This allows a development team to select precisely the best language for a subset of the problem at hand. And the approach is not limited to just programming languages. The impetus for OLE was not languages but applications. So many of the applications have OLE, DDE and DLL support. This allows direct usage of databases, spreadsheets, advanced calculators, statistic packages, graphics packages and even word processors. Multi-paradigmatic programming then opens whole new vistas for practical applications in Prolog.
Budd, T.A. (1995) Multiparadigm Programming in LEDA. Addison-Wesley.
Gonzalez, Razzazi, Shing and Zheng (1994). "On Optimal Guillotine Partitions Aprroximating Optimal d-Box Partitions", Computational Geometry: Theory and Applications, Volume 4, 1994.
Rahmani, J. (1995) "An Evolutionary Approach to Two- Dimensional Guillotine Cutting Problem," Proceedings of ICEC 95.
Samet, H. (1990) The Design and Analysis of Spatial Data Structures. Addison-Wesley, Reading, MA.
Tarnowski, A. (1992). "Exact Polynomial Algorithm for Special Case of the Two-Dimensional Cutting Stock Problem: (A) Guillotine Pallet Loading Problem", Technical Report 9205, Belarusian State University, Department of Mathematical Problems in CAD.